Causalidade é a relação entre um evento (a causa) e um segundo evento (o efeito), em que o segundo acontecimento é entendida como uma consequência do primeiro.
No uso comum, a causalidade é também a relação entre um conjunto de fatores (causas) e um fenômeno (o efeito). Qualquer coisa que afete um efeito, é denominada fator desse efeito. Um fator direto é um fator que afeta diretamente o efeito, isto é, sem quaisquer fatores intervenientes.
Compreender a relação causa-efeitoentre as variáveis é de interesse primordial em muitos campos da ciência. Normalmente, a intervenção experimental é utilizada para avaliar estas relações.
Entre os métodos comuns para a avaliação da cause e efeito destacam-se:
Pacote pcalg
Suponha que temos um sistema descrito por algumas variáveis e muitas observações obtidas deste sistema. Além disso, suponha que seja plausível a não existência de variáveis faltantes (omissão de variáveis) e também que no sistema não apresenta loops de feedback do sistema causal subjacente.
A estrutura causal de um sistema deste tipo pode ser convenientemente representado por um gráfico acíclico dirigido (DAG - Directed Acyclic Graph), em que cada nó representa uma variável e cada aresta representa uma causa direta.
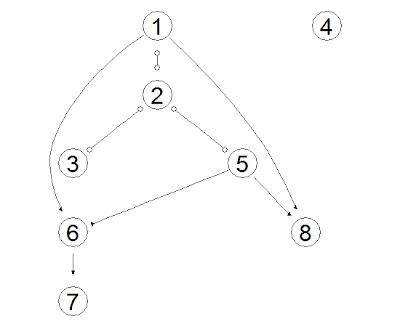
Por exemplo, suponha o seguinte grafo:
Nesse exemplo, a variável 1 causa a variável 2 diretamente, ou seja é um fator direto para a variável 2 mas é um fator interveniente da variável 5.
Usualmente, não se conhece a relação entre as variáveis a não ser que algum modelo teórico seja desenvolvido para explicar a relação entre as variáveis, e mesmo nesse caso o modelo necessita ser validado.
O caso mais comum ocorre quando não há qualquer informação quanto ao comportamento causal dessas variáveis, nesse caso o objetivo é estimar essas relações e apresentar o grafo causal estimado.
Os modelos implementados no pacote pcalg são capazes de estimar o grafo causal das variáveis de uma base de dados mesmo que nenhum modelo seja conhecido a priori.
Os métodos implementados são o Algoritmo PC (Spirtes et al., 2000), Algoritmo FCI (Spirtes et al. ,1999), Algoritmo RFCI (Colombo et al., 2012) e o Método IDA (Maathuis et al., 2009).
Alguns pressupostos para cada um dos algoritmos implementados no pacote pcalg são apresentados abaixo:
- Algoritmo PC: Nenhuma variável oculta existe ou deixou de ser selecionada.
- Algoritmo FCI: Permite a existência de variável oculta ou omissão de variáveis.
- Algoritmo RFCI: Permite a existência de variável oculta ou omissão de variáveis.
- Método IDA: Nenhuma variável oculta existe ou deixou de ser selecionada.
Prática no R.
Antes de instalar o pacote pcalg no R é necessário instalar dois pacotes:
Para a representação de gráficos, o pacote pcalg utiliza dois outros pacotes chamados RBGL e o pacote graph.
Estes pacotes não estão disponíveis no CRAN, mas estão no outro repositório do software R, BioConductor.
Para instalá-los, siga as instruções abaixo:
#Instala os pacotes necessários.
source("http://bioconductor.org/biocLite.R")
biocLite("RBGL")
biocLite("Rgraphviz")
Após a instalação desses pacotes, instale normalmente o pacote pcalg. Como exemplo utilizaremos dados simulados pelos autores do pacote pcalg.
Esses dados foram construídos de modo a possuírem a estrutura gráfica apresentada anteriormente. Aqui, realizaremos estimativas com base nos dados para avaliar se os métodos gráficos implementados no pcalg conseguem identificar corretamente a estrutura gráfica original.
Devemos inicialmente habilitar o pacote pcalg e em seguida ler o conjunto de dados que desejamos explorar:
#Habilita o pacote pcal
library("pcalg")
#Lê os dados simulados
dados.df<-read.csv("http://dl.dropbox.com/u/36068691/DadosPCALG.csv",sep=" ")
O primeiro método que utilizaremos é o Algoritmo PC:
#Gera as Estatísticas Suficientes estatisticas <- list(C = cor(dados.df), n = nrow(dados.df)) #Executa o Algoritmo PC pc.fit <- pc(estatisticas, indepTest = gaussCItest, p = ncol(dados.df), alpha = 0.01) #Plota os resultados plot(pc.fit, main = "Algoritmo PC.")Na primeira parte do comando a lista estatisticas armazena a Matriz de Correlações e o tamanho da amostra (número de observações na base). Essas informações são suficientes para a execução do Algoritmo PC. Em seguida a função pc(.) executa o Algoritmo PC. O comando "gaussCItest" testa a independência condicional assumindo que as variáveis possuem distribuição normal a um nível de significância de 0.01. O resultado obtido fornece o seguinte grafo:
#Executa o Algoritmo FCI fci.fit <- fci(estatisticas, indepTest = gaussCItest, p = ncol(dados.df), alpha = 0.01) #Plota os resultados plot(fci.fit, main = "Algoritmo FCI.")O grafo obtido usando esse algoritmo foi:
#Executa o Algoritmo RFCI rfci.fit <- rfci(estatisticas, indepTest = gaussCItest, p = ncol(dados.df), alpha = 0.01) #Plota os resultados plot(rfci.fit, main = "Algoritmo RFCI.")O Algoritmo RFCI é similar ao Algoritmo FCI. No entanto, esse é mais rápido em sua execução. O grafo produzido, nesse caso, é idêntico ao Algoritmo FCI:
#Executa o Método IDA para o Algoritmo PC ida(1, 6, cov(dados.df), pc.fit@graph)O comando retorna os seguintes valores [0.7536376 0.5487757]. Isso significa que a magnitude do efeito da variável 1 sobre a variável 6 é algum valor nesse intervalo. Uma vez que ambos os valores são maiores do que zero, podemos concluir que a variável 1 apresenta um efeito positivo causal sobre a variável 6. Esses valores refletem o efeito do aumento em uma unidade na variável 1 em relação a variável 6. Em alguns casos quando se conhece determinadas relações entre as variáveis, é possível fixar relações e permitir que os algoritmos busquem apenas as relações de causalidade desconhecidas, nesses casos utiliza-se os comandos fixedGaps e fixedEdges.
Nenhum comentário:
Postar um comentário