QGIS - Aplicações em geomarketing - Parte 3.

Nesse post mostrarei como elaborar mapas temáticos no Quantum Gis.

Mapas temáticos são úteis quando deseja-se apresentar geograficamente variáveis oriundas de algum banco de dados.

Para o exercício contido aqui é importante que o leitor tenha reproduzido os exercícios dos posts anteriores (Parte 1 e Parte 2), assim a compreensão será completa.

Elaborando mapas temáticos.

Para executar esse exercício faça o download da malha digital de columbus. No arquivo Dados Columbus.zip os principais itens são:

• Columbus.shp
• Dados.dbf

Lembrando que para trabalhar com mapas no formato digital é necessário pelo menos três arquivos: *.shp, *.shx e *.dbf. Todos com o mesmo nome, por exemplo, Columbus.shp, Columbus.shx e Columbus.dbf.

Além desses arquivos, pode ser interessante adicionar a tabela do mapa outras variáveis. No caso da malha Columbus.shp a tabela com os dados chama-se Dados.dbf.

O Quantum Gis aceita a importação de arquivos em diversos formatos, o mais comum é o formato *.dbf.

Isso não é uma restrição a sua análise, já que softwares como Excel, Access, Open Office, SPSS, SAS, R, etc. são capazes de converter suas bases nativas para o formato *.dbf.

Particularmente, o software que eu mais gosto para fazer esse tipo de conversão é o StatTransfer (o problema é que ele não é gratuito).

Realizando o JOIN entre as tabelas do mapa e base de dados.

Para realizar a união (join) entre os dados (Dados.dbf) e a malha (Columbus.shp) é necessário inicialmente que ambos os arquivos possuam uma variável chave essa variável será responsável pela determinação de quais observações da base de dados (Dados.dbf) estarão associadas aos polígonos da malha digital (Columbus.shp).

É importante que as variáveis tenham o mesmo formato, isso é, se uma é caractere a outra variável deverá ser caractere, se é numérica, ambas devem ser numéricas. Se uma tem 6 dígitos a outra também deverá ter seis dígitos.

Graficamente, podemos representar da seguinte forma:

Uma boa prática é utilizar variáveis chave que sejam numéricas. Assim evitamos problemas com acentuação, letras maiúsculas, minúsculas, etc..

Usualmente, as principais variáveis chave são:

• Código do município.
• Código do setor censitário.
• CEP.

No caso do nosso exercício, a variável chave chama-se POLYID em ambos os arquivos Dados.dbf e Columbus.shp.

Adicionando a malha no ambiente QGis.

Como demonstrado nos posts anteriores, admita que a malha já esteja projetada e adicionada no ambiente QGis.

Graficamente, devemos ter algo como:

Em seguida devemos fazer a junção (join) entre os dados (Dados.dbf) e a malha (Columbus.shp) para isso arraste o arquivo Dados.dbf para o ambiente QGis. Essa base aparecerá no campo Layers como mostrado abaixo:

Em seguida, clique com o botão direito do mouse sobre o Layer columbus e escolha a opção Properties. Na tela que surge clique na aba Joins.

Clique no botão "soma" e assim surgirá o seguinte formulário:

A variável chave em ambos os campos é POLYID. Em seguida clique no botão OK:

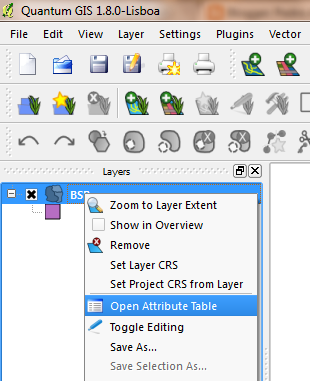
Finalmente, clique no botão Apply e posteriormente no botão OK. Para saber se as variáveis foram adicionadas corretamente, clique com o botão direito do mouse sobre o Layer columbus e escolha a opção Open Attribute Table. Se o procedimento foi realizado corretamente, haverá novas variáveis na base de dados do Layer columbus. Essa malha com novas variáveis pode ser salva, evitando assim a repetição de procedimento no futuro.

Pintando o mapa.

Agora, podemos visualizar a distribuição da criminalidade em Columbus, para isso, faremos um mapa temático.

O primeiro passo é clicar com o botão direito do mouse sobre o Layer columbus e escolher a opção Properties. Na tela que surge escolha a aba
Style:

Escolha então a opção Graduated:

Na caixa Column escolha a variável que desejamos representar espacialmente (aqui será a variável CRIME), na caixa Mode há algumas opções, aqui escolheremos a opção Natural Breaks (Jenks) que minimiza a variância interna em cada uma das classes. O número de classes escolhidas aqui é 5 e pintaremos o mapa na escala de laranjas:

Clique no botão Apply e posteriormente no botão OK. O resultado é o seguinte:

Para exportamos o mapa final para um formato de imagem procedemos da seguinte forma: clique no botão New Print Compose:

Na tela que surge, clicamos no botão Add New Map e com o mouse definimos onde gostaríamos que o mapa estivesse na imagem:

Usando o mouse representamos onde o mapa deverá estar:

Para adicionar a legenda, clicamos no botão Add new legend:

Novamente usando o mouse posicionamos onde a legenda deverá estar. Por fim usando a janela Item properties podemos editar as opções da legenda:

Para salvar o mapa fazemos File → Export as PDF.... É claro que você pode salvar a imagem em outros formatos também.

Previsão de Séries Temporais usando Holt Winters.

Usualmente, quado desejamos fazer previsão há uma série de informações sobre o mercado que deveríamos levar em conta. Por exemplo, as vendas de produtos são muitas vezes sazonais, e podemos esperar que as tendências sejam sustentadas por períodos curtos, os quais podem se alterar.

Se temos por exemplo um produto inovador bem-sucedido, as vendas aumentarão inicialmente, mas depois estabilizarão antes de decrescer devido aos concorrentes que entram no mercado. Esse tipo de informação pode ser adequadamente modelada pelo método Holt-Winters.

A nomenclatura usada aqui define a mudança no nível de um período de tempo para o período seguinte, como inclinação (slope). Os padrões sazonais também podem mudar devido aos caprichos da moda e da variação do clima.

O método de Holt-Winters foi sugerido por Holt (1957) e Winters (1960), que
trabalharam no School of Industrial Administration em Carnegie Institute
of Technology.

O método usa médias móveis ponderadas exponencialemente para atualizar as estimativas da média ajustada sazonalmente (chamada de nível), inclinação e sazonalidade.

Considere uma série temporal $\{x_{t}\}$ com período igual a $p$. O método Holt-Winters utiliza as seguintes equações:

onde $a_{t}$, $b_{t}$ e $s_{t}$ são as estimativas para o nível, inclinação e efeito da sazonalidade no período $t$. Os parâmetros $\alpha$, $\beta$ e $\gamma$ são os parâmetros de suavização.

A previsão para valores futuros $x_{n+k}$ em $k$ períodos a frente após a $n$-ésima observação é dada da seguinte forma:

onde $a_{n}$ é o nível estimado, $b_{n}$ é a inclinação estimada e $a_{n}+kb_{n}$ é o nível estimado no tempo $n+k$ e $s_{n}+k-p$ é a estimativa do peso exponencializado para o efeito sazonal no tempo $n=k-p$. Outra forma do método Holt-Winters é com efeito sazonal multiplicativo. Nesse caso, o conjunto de equações é dado por:

A equação de previsão para o período $x_{n} + k$ torna-se:

Os parâmetros podem ser fixados no R ou então estimados de modo a minimizar o erro de previsão. Em outras palavras, quando os parâmetros não são informados, o R procura pelos valores que minimizam o erro de previsão.

Usando o método Holt-Winters no R.

Para realizar a estimação e posterior previsão pelo método Holt-Winters no R utilizamos a função HoltWinters.

Para esse exemplo, considere a base de dados das concentrações atmosféricas de CO2 expressos em partes por milhão (ppm).

O nome da base em CSV é denominada BaseCO2.csv.

O primeiro passo é ler a base de dados no R:

#Lê a base de dados
dados.df<-read.csv("http://dl.dropbox.com/u/36068691/BaseCO2.csv")

#Imprime as variáveis existentes
names(dados.df)

#Cria a série temporal
serie<-ts(dados.df$CO2,start=c(1959,1),end=c(1997,12),frequency=12)

Os dados também foram transformados no formato ts com a primeira observação referente a Janeiro de 1959 e a última em Dezembro de 1997. O argumento frequency=12 informa ao R que cada período (de um ano) é composto por 12 observações. Em outras palavras, informa ao R que a frequência da série é mensal. Em seguida utilizamos a função HoltWinters:

#Realiza o método Holt-Winters
holt <- HoltWinters(serie)

#Plota a série temporal
plot(holt)

#Plota a decomposição da serie
plot(fitted(holt))

A série temporal observada juntamente com seus valores preditos pelo modelo são representados no gráfico abaixo:

O método decompõem a série temporal. Essa decomposição é apresentada a seguir:

A previsão para o próximo ano com um intervalo de confiança de 95% é dado pelo seguinte comando:

#Realiza a previsão para 12 meses a frente
p <- predict(holt, 12, prediction.interval = TRUE, level = 0.95)
plot(holt, p)

Cujo resultado é apresentado pelo gráfico abaixo:

Caso não haja sazonalidade evidente, podemos fazer:

#Realiza o método Holt-Winters sem efeito sazonal
holt <- HoltWinters(serie, gamma = FALSE)

Para maiores detalhes do método Holt-Winters indico o texto The Holt-Winters Forecasting Procedure.

QGIS - Aplicações em geomarketing - Parte 2.

Dando continuidade sobre as operações no Quantum Gis em especial com aplicações em Geomarketing demonstrarei aqui como adicionar ao mapa: ruas ou imagens de satélites oriundas do Google Maps.

Esse tipo de análise é útil quando deseja-se estudar o impacto de variáveis georeferenciadas e a sua relação com possíveis estruturas como ruas, shoppings, parques, etc..

Assumindo que a primeira parte do post QGIS - Aplicações em geomarketing - Parte 1, tenha sido realizada podemos seguir aqui com uma nova análise.

Adicionando Layers do Google Map no QGis.

Considere a malha de setor censitário de Brasília, a mesma malha publicada no post QGIS - Aplicações em geomarketing - Parte 1.

Após realizar a projeção em: Projected Coordinate Systems → Universe Transverse Mercartor (UTM) → SAD69/ UTM Zone 23S (procedimento explicado no primeiro post) e ter salvo a nova malha já projetada, a tela do Qgis deverá ser algo como:

Para adicionar a malha do Google Map no Qgis precisamos adicionar um plugin no Qgis.

Os plugins são compilações de funções, usualmente criadas pelos usuários do Qgis que realizam determinadas tarefas.

O primeiro passo para adicionar a malha do Google Map no Qgis precisamos adicionar um novo repositório de plugins no software.

Para isso, execute os seguintes procedimentos: Plugins → Fetch Python Plugins... na tela que surgir escolha a aba Repositories, a seguinte surgirá:

O plugin que necessitamos chama-se OpenLayers Plugin.

Para que ele fique disponível, precisamos adicionar o seguinte repositório: http://build.sourcepole.ch/qgis/plugins.xml. Para isso, clique no botão Add e adicione o nome do repositório (por exemplo, Repositorio) e o endereço (nesse caso http://build.sourcepole.ch/qgis/plugins.xml) e clique no botão OK:

Na aba plugins procure pelo plugin OpenLayers e adicione-o. Para isso, clique nele e pressione o botão Install plugin:

Após esse procedimento, feche a janela. Em seguida, para adicionarmos a malha do Google Map no ambiente do Qgis faça no Menu: Plugins → OpenLayers plugin → Add Google Streets layers:

Como o QGis funciona como um sistema de camadas (Layers) a camada superior se subrepõem as demais, assim, caso a malha BSB esteja sobre a malha Google Streets a seguinte imagem surge:

Para trocar a ordem das camadas basta segurar a camada desejada e arrastar para a posição de interesse. Entretanto, não é possível observar as ruas sobre a malha BSB, para isso, podemos reduzir a visibilidade da camada BSB.

Para isso, dê dois cliques com o botão direito sobre a cor do Layer BSB (nesse caso o quadrado em lilás), caso o procedimento tenha sido executado corretamente a seguinte tela surgirá:

Faça a transparência igual a 50%:

Em seguida clique no botão OK:

Com a transparência alterada para 50% boa parte das estruturas existentes no Google Street podem ser observadas nesse novo mapa e análises podem ser formuladas com base nesse novo mapa.

Teste de razão de variâncias de Lo-MacKinlay.

Existem muitos textos que sugerem através de evidências empíricas que o retorno de ações contém componentes que podem ser preditos.

Por exemplo, Keim e Stambaugh (1986) encontraram um modelo estatisticamente significante para prever o preço de ações usando um modelo de previsão com variáveis pré-determinadas.

Fama e French (1987) mostraram que um longo período de retenção de retornos é negativamente correlacionado serialmente, implicando assim que 25% a 40% da variação de um longo período de retornos é previsível com base nos retornos passados.

Esse post, no entanto, tem como objetivo principal apresentar o Teste de Razão de Variâncias proposto por Lo e MacKinlay (1988). Os autores indicam que o modelo de passeio aleatório (ou passeio do bebâdo) é, em geral, inconsistente (para os ativos estudados) com o comportamento estocástico dos retornos semanais, especialmente para as ações com menor capitalização (Small Caps).

Lo e MacKinlay (1988) alertam que estes resultados não implicam necessariamente que o mercado de ações é ineficiente ou que os preços das ações não são avaliações racionais dos seus valores "fundamentais". O teste proposto pelos autores pode ser interpretado como um teste para a rejeição de "algum" modelo econômico de formação eficiente de preços.

Teste de razão de variâncias.

A eficiência do mercado de ações tem sido debatida por pesquisadores e profissionais do mercado financeiro. Uma forma particular de eficiência do mercado de ações é a eficiência informacional.

A eficiência informacional se baseia na premissa de que os preços dos ativos refletem as informações relevantes disponíveis instantaneamente aos investidores e ao público em geral. Como a chegada de informações é imprevisível, os preços dos ativos também se tornam imprevisíveis. A hipótese de que a chegada de informações fundamentais ao mercado é aleatória e, portanto, os movimentos dos preços dos ativos também serão aleatórios, é englobada pela teoria do passeio aleatório dos preços dos ativos.

De maneira simplista, a teoria do passeio aleatório indica que uma vez que a chegada de informações é imprevisível, o melhor preditor do preço de um ativo é seu valor atual. Esta ideia simples pode ser facilmente incorporada no modelo de passeio aleatório bem conhecido dos preços dos ativos, que pode ser expresso da seguinte forma: $P_{t}=P_{t-1}+\epsilon$.

$P_{t}$ é o preço atual do ativo em estudo, $P_{t-1}$ é o preço do período anterior, e $\epsilon$ é um termo de erro aleatório. Cada termo de erro aleatório representa a chegada de uma nova informação, o qual se assumido ser imprevisível deve ser independentes uns dos outros. Admitindo sobre a hipótese nula o termo de erro aleatório é independente e identicamente distribuído segundo uma distribuição normal, então a variância do termo de erro aleatório é linear no intervalo de tempo durante o qual os preços são observados. Simplesmente, a variância da variação de preços quinzenais deve ser o dobro da variação de preços semanais. Além do mais, a variância das alterações de preços mensais deve ser quatro vezes superior ao de alterações de preços semanais, e assim por diante.

A relação linear entre o intervalo de tempo observado para os preços do ativo de interesse e a sua variação é a essência da especificação do teste desenvolvido por Lo e MacKinlay (1988). Lo e MacKinlay (1988) desenvolveram distribuições limitantes para os estimadores de razão de variância, com e sem a existência de heterocedasticidade, e mostraram que os preços dos ativos não necessariamente seguem um passeio aleatório. Seus estimadores são definidos como se segue:

A equação (01) representa a média das alterações dos preços em T períodos de tempo:

Já a equação (02) representa um estimador de variância para as alterações dos preços no period de tempo especificado, isso é $t=1,\dots,T$:

Por fim, a equação (03) representa um estimador de variância para as mudanças q-temporais de preços:

e $m=q(T-q+1)(1-\frac{q}{T})$ é um ajuste executado no denominador da variância do estimador q-temporal para acomodar as observações que se sobrepõem, além de ajudar a aumentar a potência do teste de razão de variância.

Especificação do teste.

Assim, o teste da razão de variâncias é definido por:

Para acomodar a possível heterocedasticidade, utiliza-se a estatística do teste padronizado $z$ o qual é assintoticamente distribuído segundo uma normal padrão:

onde

e

Aplicação usando os dados da Bovespa

Utilizando o R, vamos calcular o teste de razão de variâncias de Lo e MacKinlay para as ações PETR4 em um período $q=1$ diário, isso é, com defasagem de um dia.

#Limpa o console
rm(list=ls(all=TRUE))

#Habilita o pacote quantmod
library(quantmod)

#Início do período de interesse
start = as.Date("2011-01-01") 

#Fim do período de interesse
end = as.Date("2011-12-31") 

#Obtêm os dados da PETR4
getSymbols("PETR4.SA", src="yahoo",from=start,to=end)

A seguir é necessário calcular os log-retornos de duas séries: a série original e a série defasada (nesse caso em um dia):

#Aplica o log-retorno nos preços
ret <- as.matrix(c(rep(NA, 0), diff(log(Cl(PETR4.SA)), lag=1)))

#Aplica o log-retorno nos preços (Defasagem diária)
ret2 <- as.matrix(c(rep(NA, 0), diff(log(Cl(PETR4.SA)), lag=2)))

#Plota a série temporal dos preços de fechamento
plot(ret, main="Petr4",type="l",
+ylab="Log-return Close price. (Lag 1)",xlab="Time")

plot(ret2,main="Petr4",type="l",
+ylab="Log-return Close price. (Lag 2)",xlab="Time")

Em seguida os parâmetros exigidos para o teste são calculados:

#Calcula muhat
muhat <- mean(ret, na.rm=TRUE)
nq <- nrow(ret)

#Parâmetros Sigma e Delta
sigatop <- (ret - muhat)^2
sigatop1 <- c(NA, sigatop[-length(sigatop)])
deltop <- sigatop * sigatop1
delbot <- sigatop
sigctop <- (ret2 - 2*muhat)^2

#Guarda os resultados
dados <- data.frame(ret, sigatop, sigatop1, deltop, delbot, sigctop)

Fazendo a soma, obtemos os valores desejados:

#Calcula a soma dos valores
sigatop <- sum(sigatop, na.rm=TRUE)
sigctop <- sum(sigctop, na.rm=TRUE)
deltop <- sum(deltop, na.rm=TRUE)
delbot <- sum(delbot, na.rm=TRUE)

Em seguida o cálculo dos testes é realizado:

nq<-nrow(ret)
q<-2
qm1<-q-1
theta<-0
j<-1
m <- q*(nq-q+1)*(1-q/nq)
siga <- sigatop/(nq-1)
sigc <- sigctop/m
varrat2 <- sigc/siga
delta <- nq*deltop/(delbot**2)

while(j <= qm1)
{
  theta <- theta + ((2*(q-j)/q)**2)*delta
  j<-j+1
}

z <- sqrt(nq)*(varrat2-1)/sqrt(theta)
print(nq, cat("Número de retornos:"))
print(varrat2, cat("Razão de variâncias para retronos com Lag=2:"))
print(z, cat("Teste Robusto a Heterocedasticidade de Lo-MacKinlay:"))

Após realizar a análise obtêm-se:

• Número de retornos:[1] 249
• Razão de variâncias para retronos com Lag=2:[1] 1.081269
• Teste Robusto a Heterocedasticidade de Lo-MacKinlay:[1] 1.052326

Os resultados indicam que a hipótese nula de presença de um comportamento como um passeio aleatório para a série PETR4 diária entre 01-01-2011 até 31-12-2011 não pode ser rejeitada, uma vez que o valor do teste não é maior do que o valor crítico sobre a hipótese nula, qual seja, aproximadamente 1.96 a um nível de confiança de 95%. Uma maneira direta de se atingir o mesmo resultado é por meio da biblioteca vrtest. A função que realiza o teste de Lo-MacKinlay é a função Lo.Mac(y=, kvec=) onde o parâmetro y= recebe o vetor de ativos e kvec= a defasagem utilizada no teste.

QGIS - Aplicações em geomarketing - Parte 1.

Quantum GIS (freqüentemente abreviado QGIS) é um sistema multi-plataforma livre e de código aberto para a análise de Sistemas de Informação Geográfica (SIG), que fornece dados de visualização, edição além de capacidades para análise.

A utilização de sistemas SIG em administração possui diversas aplicações, a principal é em Geomarketing.

Geomarketing é a integração de sistemas geográficos em vários aspectos de marketing, incluindo vendas e distribuição.

A pesquisa em Geomarketing é usualmente realizada por meio do uso de parâmetros geográficos em metodologia de pesquisa de marketing, incluindo amostragem, coleta de dados, análise e apresentação.

A base central de Geomarketing é o mapa digital, representado usualmente por um arquivo shapefile. No Brasil, o principal fornecedor de malhas digitais é o IBGE. Para baixar as malhas vá ao endereço ftp://geoftp.ibge.gov.br/malhas_digitais.

Vale realçar que não basta baixar apenas o arquivo em formato *.shp, mas na mesma pasta é necessário a existência de pelo menos outros dois arquivos: *.shx e *.dbf

O geomarketing é uma disciplina dentro da análise de marketing que usa geolocalização (informação geográfica) no processo de planejamento e implementação de atividades de marketing.

Esse campo pode ser usado em qualquer aspecto do mix de marketing - o produto, preço, promoção, ou praça (segmentação geográfica).

Segmentos de mercado também se correlacionam com a localização, e isto pode ser útil na gestão de marketing. O geomarketing já é uma metodologia aplicada com sucesso no setor financeiro através da identificação de caixas eletrônicos geradores de tráfego e criação de hotspots baseados em parâmetros geográficos integrados com o comportamento do cliente.

Nesse post, mostrarei um exemplo de como utilizar o Quantum GIS para a uma análise simples do mercado de escolas em Brasília.

Utilizando o Quantum GIS.

Antes de fazer qualquer análise é necessário que se saiba qual a região deseja-se estudar. No exemplo desse post trabalharemos com o setor censitário do IBGE para Brasília em 2010.

Baixe a malha de Brasília em 2010 e extraia todos os arquivos em uma mesma pasta (53SEE250GC_SIR.shp, 53SEE250GC_SIR.shx, 53SEE250GC_SIR.dbf e 53SEE250GC_SIR.prj).

Vá ao menu e escolha Layer → Add Vector Layer. É posível também adicionar o Layer apenas arrastando o arquivo 53SEE250GC_SIR.shp para o ambiente Quantum GIS Desktop.

Após a escolha da opção Add Vector Layer a seguinte tela surge:

Há três opções disponíveis:

1. File: Abre apenas um único shapefile.
2. Directory: Abre todos os arquivos shapefile presentes no diretório indicado.
3. Database: Abre os shapefile que estão em formato de base de dados.
4. Protocol: Abre o layer por meio de protocolos.

Aqui trabalharemos com a opção File. Na opção Dataset o endereço do shapefile deve ser especificado e na opção Enconding a formatação dos caracteres do Layer deve ser especificado (caso não saiba qual formatação usar utilize a opção System).

Caso tenha dado certo a seguinte imagem surgirá:

Definindo a projeção da malha para mapas no Brasil.

Antes de mais nada, vamos adicionar ao mapa uma Scale Bar. Para isso vá em View → Decorations → Scale Bar.

Surgirá a seguinte tela:

Marque a opção Enable Scale Bar. A escala surgirá no canto superior direito do QGis Desktop. O próximo passo é definir a projeção da malha digital. No canto inferior direito da tela do QGis Desktop clique no ícone CRS Status:

A seguinte tela surgirá:

Marque a opção Enable "on the fly" CRS Transformation e escolha a opção Projected Coordinate Systems → Universe Transverse Mercartor (UTM)
→ SAD69/ UTM Zone 23S

As opções produzem a seguinte tela:

Clique em Apply e depois OK. A escala agora deve estar em quilômetros e agora podemos trabalhar com essa nova projeção.

É necessário salvar esse mapa projetado e então trabalhar com o mapa salvo. Para isso clique com o botão direito no Layer e escolha a opção Save as....

Defina o local para salvar o novo arquivo em Browse, aqui denominado BSB.shp e na caixa de texto CRS clique no botão Browse e escolha a opção Projected Coordinate Systems → Universe Transverse Mercartor (UTM)
→ SAD69/ UTM Zone 23S. Depois clique em OK.

Remova o Layer antigo do ambiente QGis Desktop (basta clicar com o botão direito sobre o Layer e escolher a opção Remove) e adicione o novo Layer BSB.shp.

Selecionando polígonos em uma determinada distância.

Suponha que queiramos selecionar os polígonos que estão a uma distância (em raio) de até 10 quilômetros de uma determinada região. Ou seja, essa pode ser a influência do nosso produto e por isso desejamos estudar as regiões que estão a esse alcance geográfico.

Particularmente, suponha que queiramos obter todos os polígonos que estão a 10 quilômetros do polígono com número do setor censitário igual a CD_GEOCODI=530010805230054.

O primeiro passo é selecionar o polígono de interesse, para isso, clique com o botão direito no Layer BSB e escolha a opção Open Attribute Table:

A seguinte tala surgirá:

Para selecionarmos o polígono de interesse na caixa de texto Look for coloque o número de polígono desejado (530010805230054) e na Combo Box ao lado de in escolha a variável CD_GEOCODI em seguida clique na opção Search:

O polígono selecionado estará sublinhado de azul na tabela de dados, após esses passos feche a tabela no botão Close. O setor censitário escolhido estará realçado no mapa:

O próximo passo é salvar apenas o polígono desejado, para isso, clique com o botão direito no Layer BSB e escolha a opção Save selection as...:

Dê o nome de Selecionado.shp, escolha o local onde será salvo e confira se o CRS possui a mesma projeção do mapa, isso é: SAD69/ UTM Zone 23S.

Adicione o novo Shapefile no ambiente QGis Desktop:

Para selecionar os polígonos que estão a uma distância de 10 Km do setor censitário em verde, precisamos agora encontrar o centroide do polígono. Para isso, vá ao menu do QGis Desktop e escolha as opções: Vector → Geometry Tools → Polygon centroids , na caixa de texto Input polygon vector layer escolha o Layer: Selecionado.shp e defina o Layer que conterá o centro de massa do setor censitário desejado, no nosso caso denominamos de Centroid.shp:

Caso o procedimento tenha sido realizado de maneira correta, o centroide estará presente no mapa:

Para selecionar os polígonos que estão a uma distância de 10 Km (10000 metros) do setor censitário de interesse, vá ao menu e escolha as opções: Vector → Geoprocessing Tools → Buffer(s).

Escolha o Layer: Centroid.shp informe o raio desejado (10000 metros) e dê o nome do novo Layer com a circunferência de 10Km em relação ao setor censitário escolhido, aqui demos o nome de Raio10.shp:

O novo Layer com um raio de 10 Km surgirá:

Por fim, procuramos pela interseção entre os Layers: BSB e Raio10. Para obter essa interseção vá ao menu e escolha as opções: Vector → Data Management Tools → Join Attributes by location:

em seguida clique no botão OK. Os Layers: BSB e Raio10 são escolhidos e a malha final (Final.shp) com a interseção dos polígonos que possuem distância de seus centroids até o centroid do setor censitário de interesse de 10 Km é produzido:

Podemos retirar a seleção dos Layers que não nos interesse e dexar somente os Layers: BSB e Final habilitados: